ACADEMIC WORK
ACADEMIC WORK
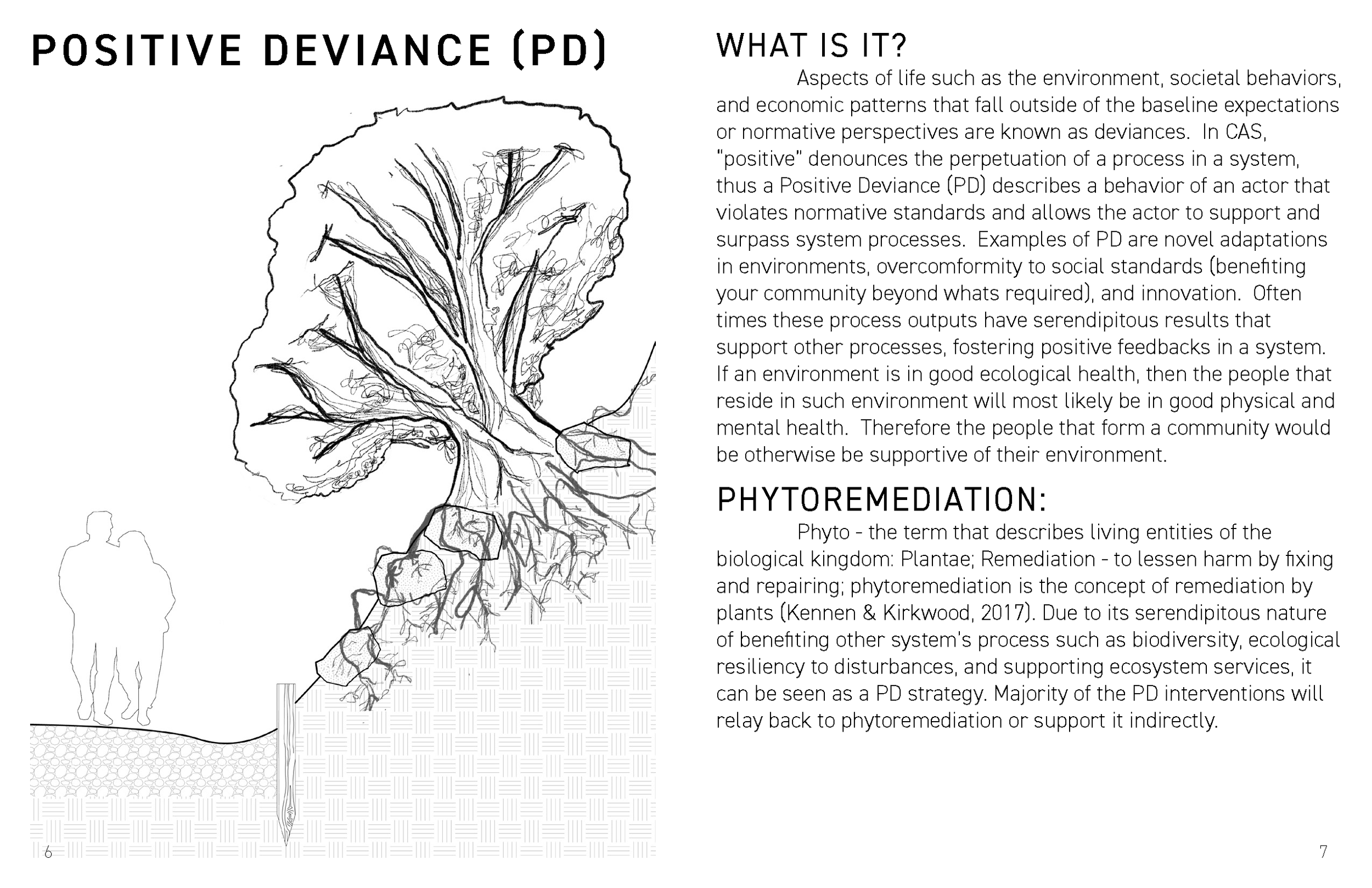
Chaos Design
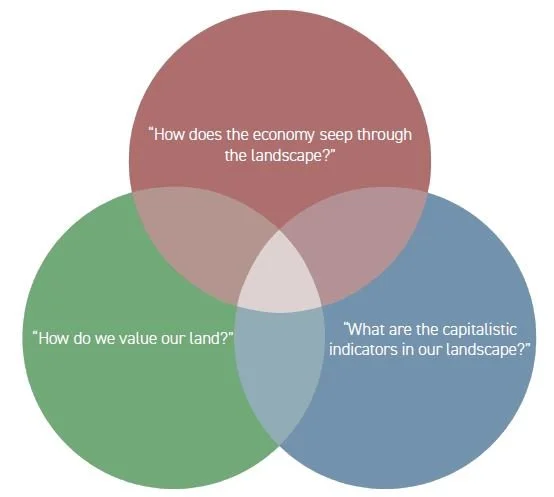
This graduate project explores chaos theory as a design framework for landscape architecture and other fields of design. It is discussed that due to the Anthropocene, the economic, social, andecological systems are hyper-connected with one another, however it is the economic system that is dictating social welfare and ecological health. I argue that this creates a situation where urban planning and landscape design is highly dependent on monetary goals, which perpetuates monetary inequity, social inequality, and climate change. I also identify that landscapes are dynamic, yet built to be static without the ability to serve people’s changing needs. The overarching inquiry examines chaos theory’s potential to challenge the economic-centric system, to address social needs, and to offer sustainable solutions to climate change. Design interventions will mimic chaotic behaviours and processes found in complex adaptive systems. The interventions will take form as a zine booklet for users to take agency and to manifest their needs in their landscape.
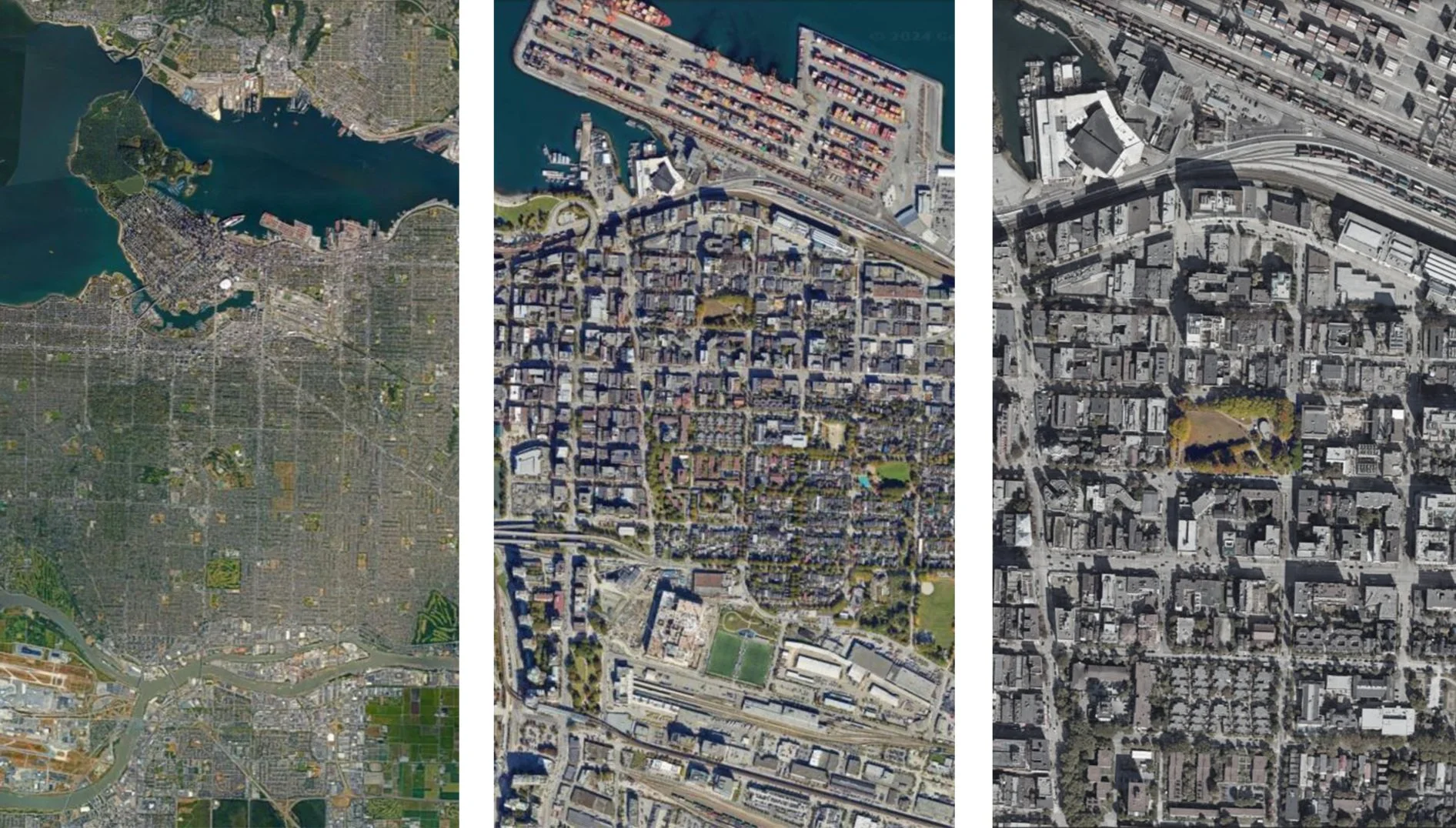
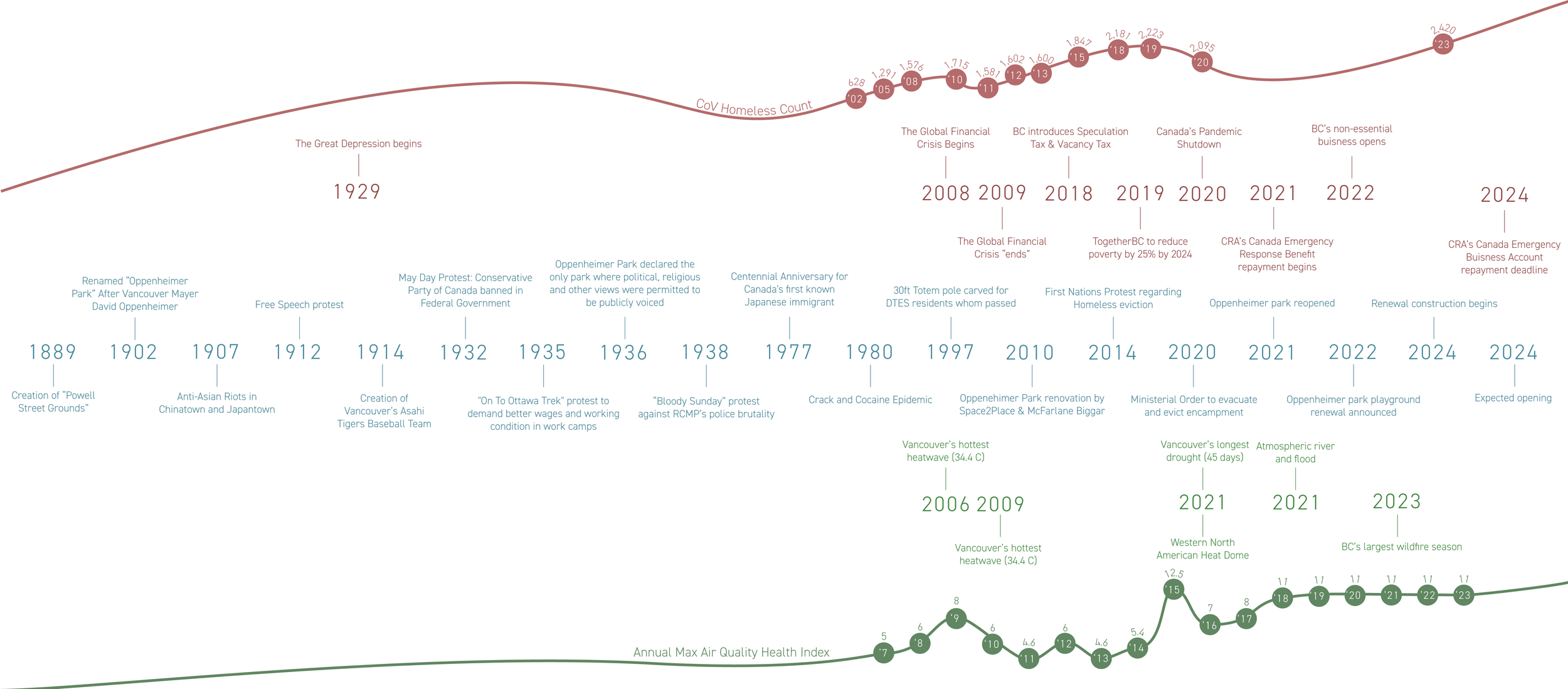
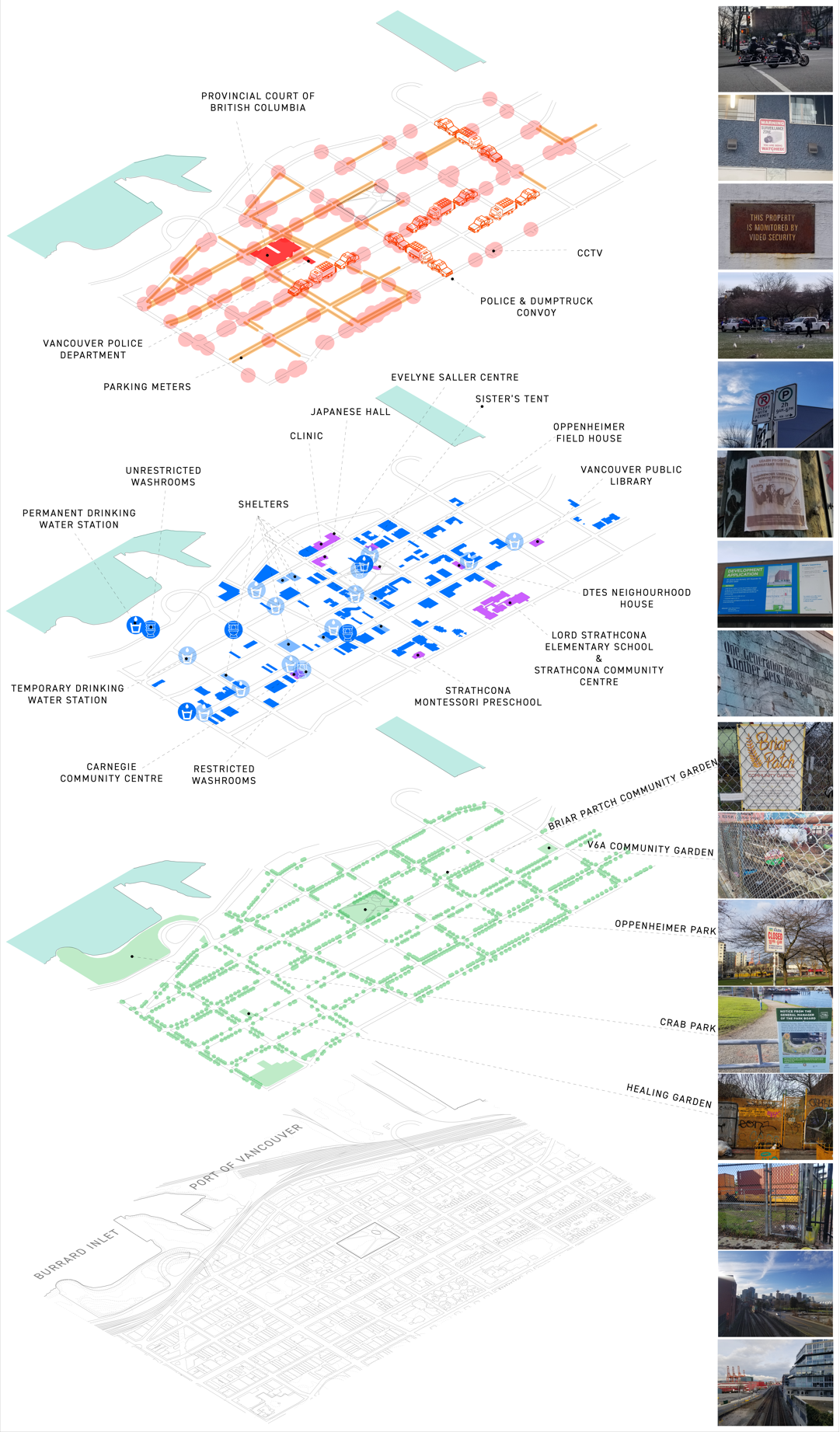
Gentrification and zoning dictates the value of the landscape. Biased carceral oversight limits the freedom to use already-limited third spaces. Ecological health is suppressed by the site’s industrial history. Oppenheimer Park, in Vancouver, BC, is selected to experiment on how these interventions will unfold onto society. Part of the inspiration for choosing Oppenheimer Park is my personal relationship with the Downtown Eastside. As a teenager, my highschool provided many opportunities for us to volunteer in the area, and as a tradition my family and I serve at the soup kitchen named “the door is open” every Christmas. Through my ongoing weekly volunteer sessions since December, along with my observation and conversation with guests and other volunteers, I understood that Oppenheimer Park is not only a contentious site, but a significant place of refuge, safety, and ongoing community engagement. The system of Oppenheimer Park will be modeled as a Strange Attractor. Design interventions will alter the attractor’s parameters to test how it will behave in a simulation, giving landscape architects a framework on how their design goals may impact the landscape. Similar to how landscape architects may use history to gauge validity of a design, this framework anticipates how interventions will unfold in a dynamic landscape.
Graduate Supervisor
Sara Jacobs
Year
2024
Site
Oppenheimer Park, Vancouver BC
Highlights
Chaos Theory, Strange Attractors, Complex Adaptive Systems, Solidarity and Justice, Economy, Sociology, Ecology, Policy, Design Framework, Tool Kit
Concept Collage
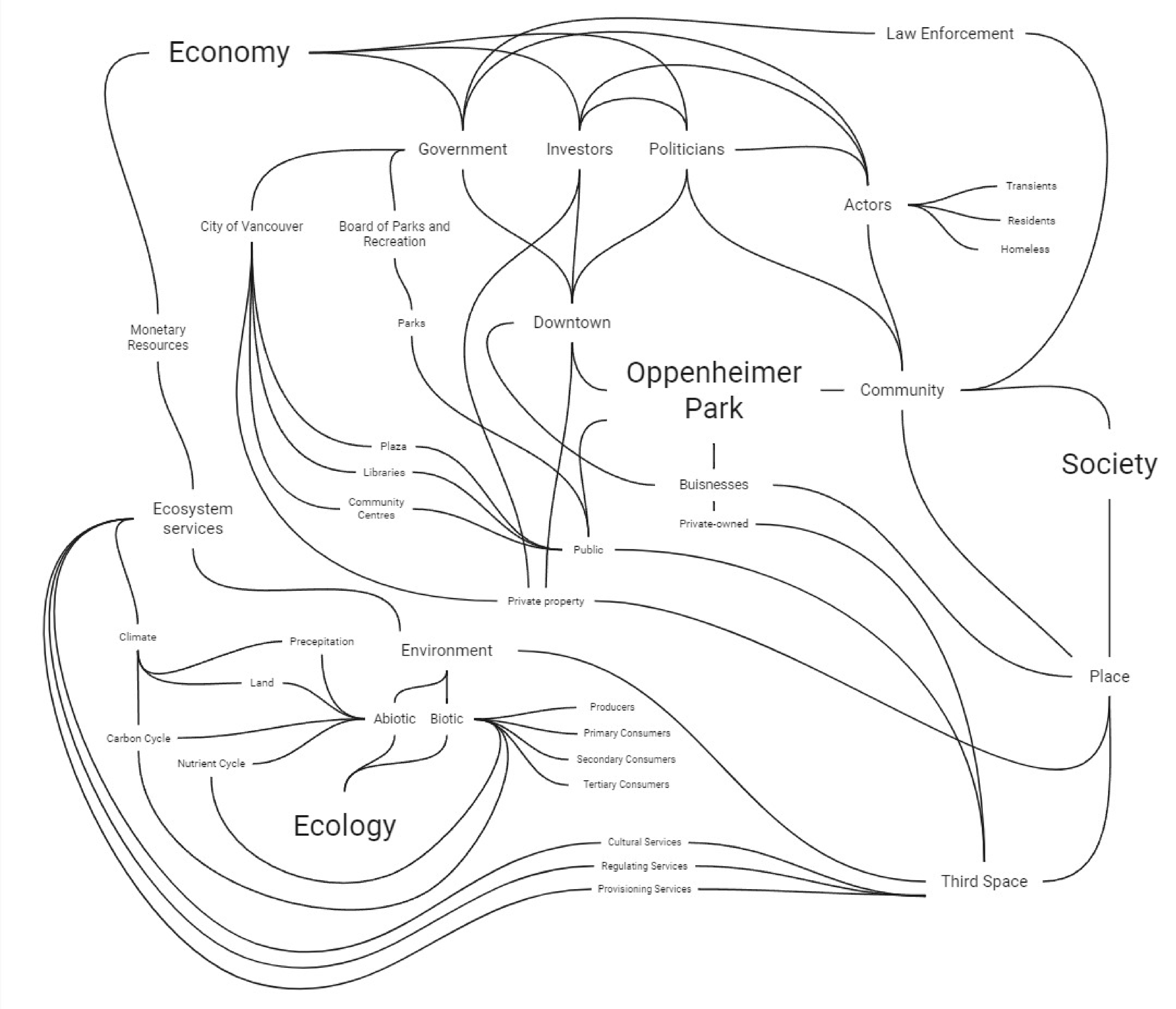
Three Acting-Systems Diagram
Site Context
Systems Timeline
Isometric Systems Analysis
Economic System Collage
Social System Collage
Ecological System Collage
System-Based Guiding Questions
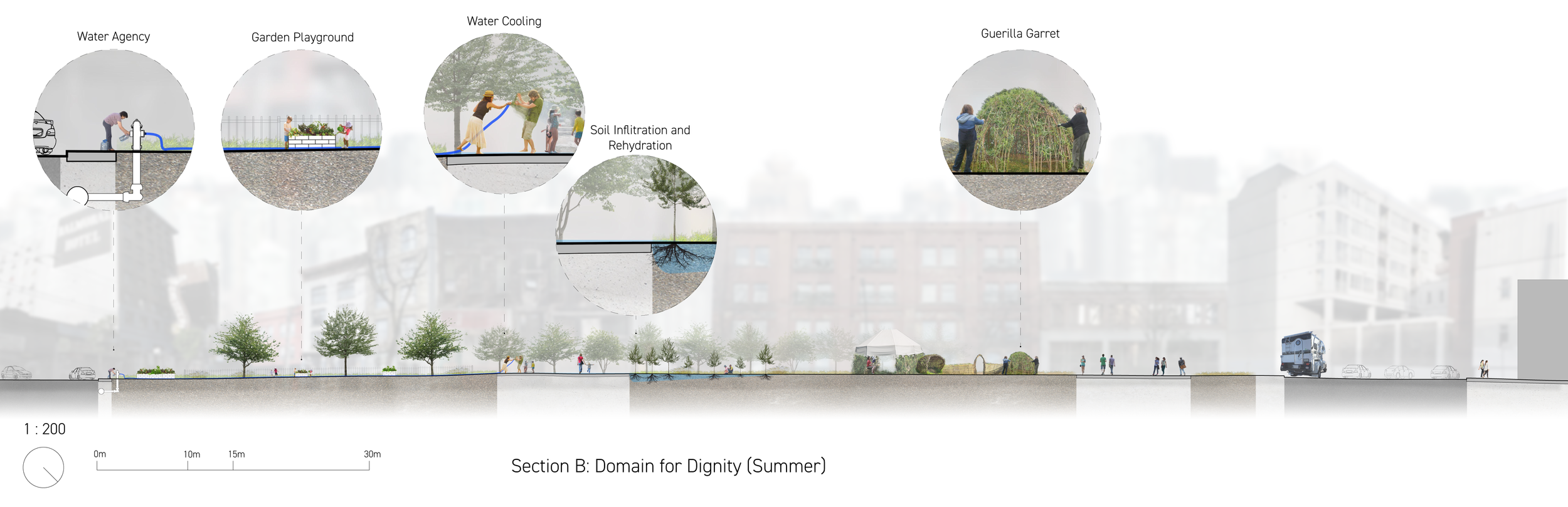
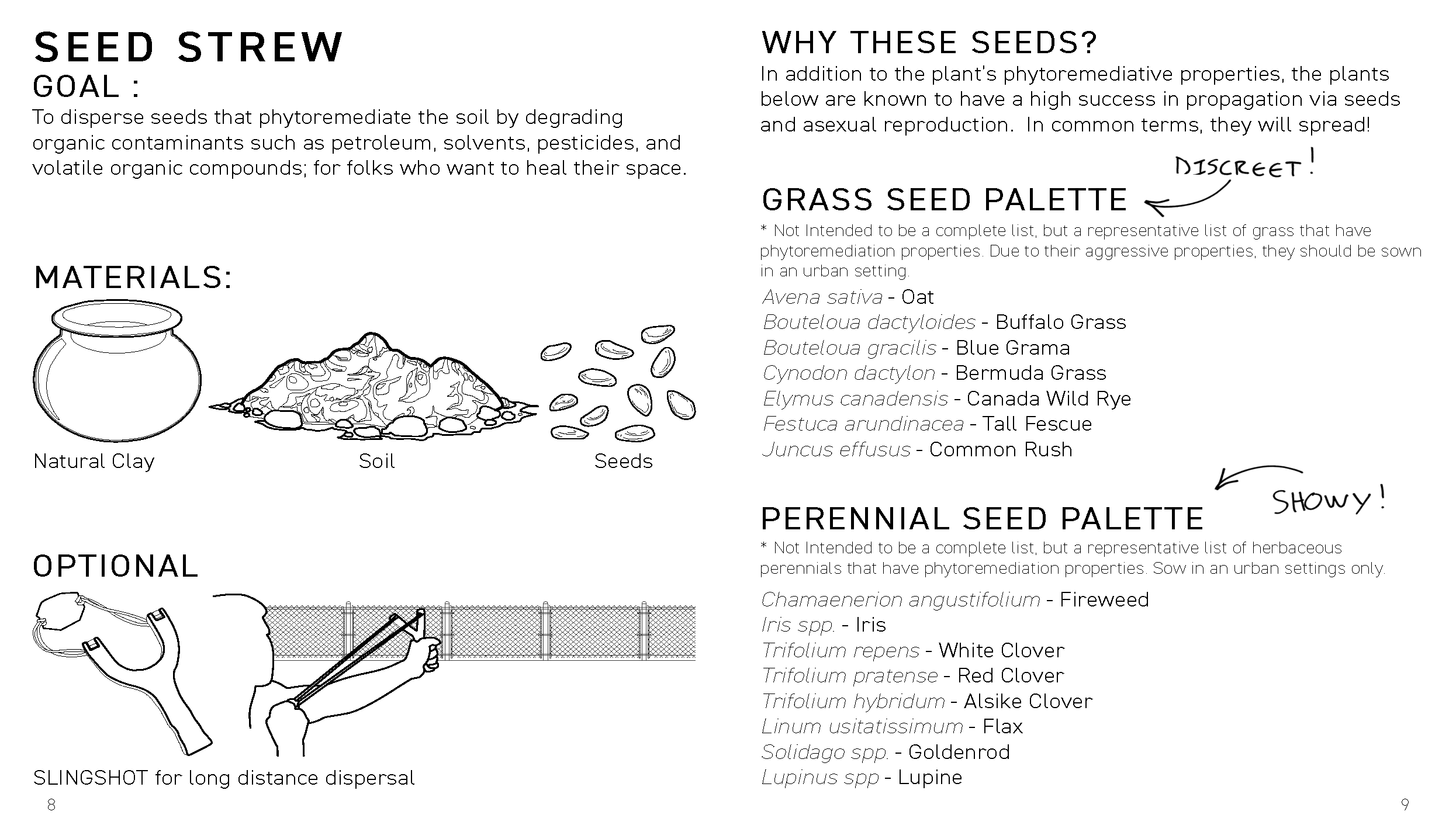
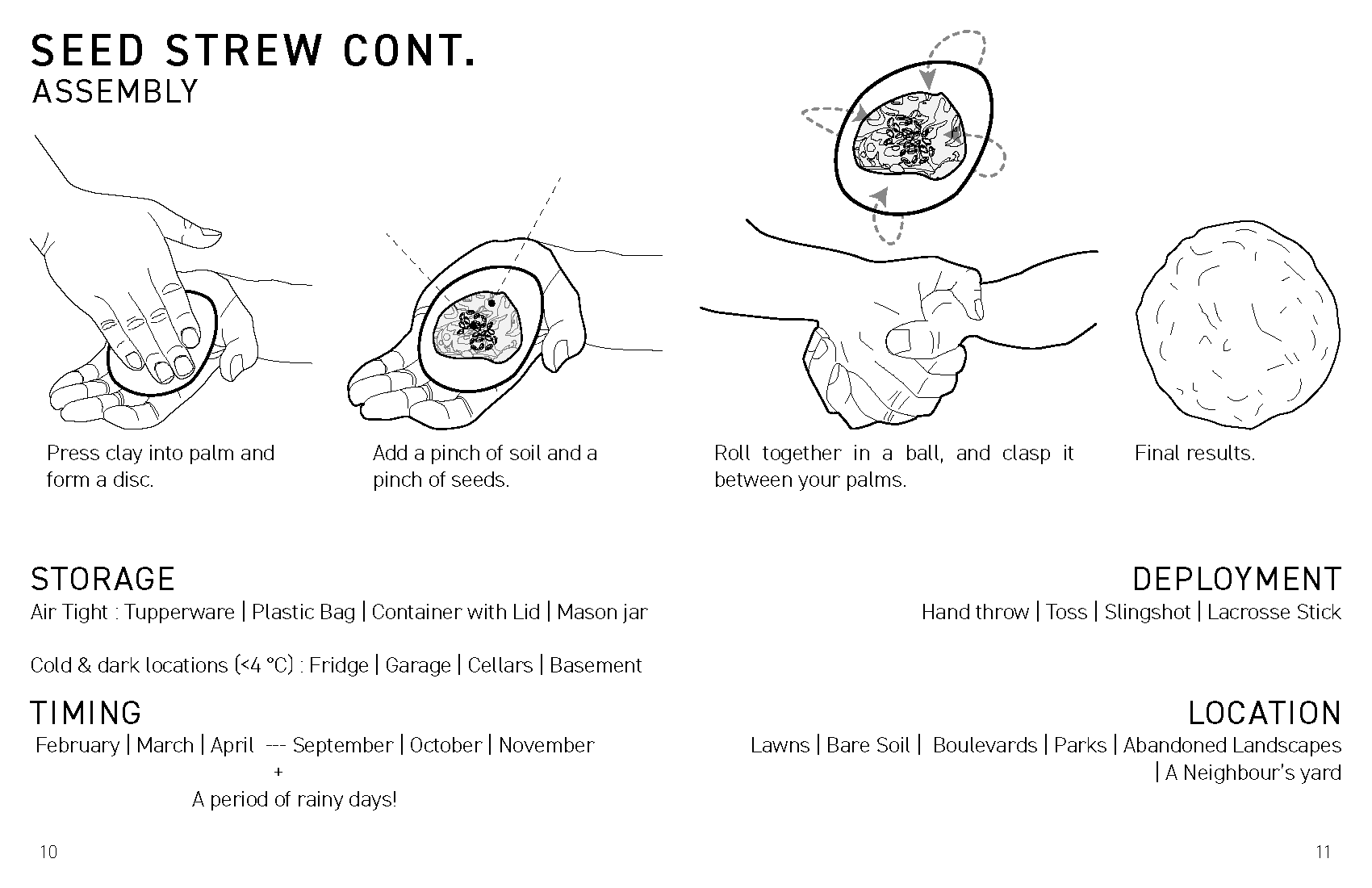
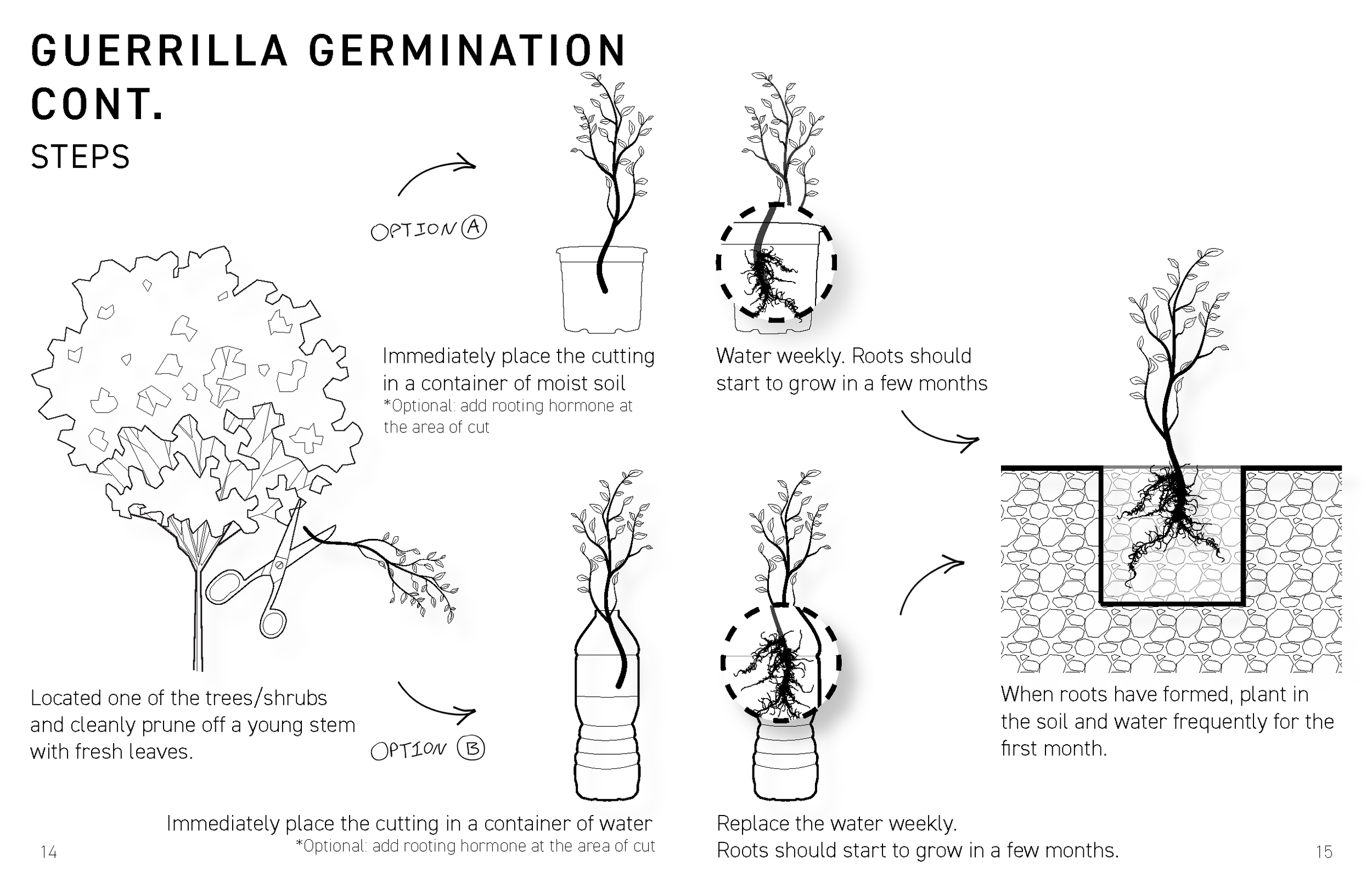
Zine - “Chaos Catalogue”
The Downtown East Side Web
The DTES Attractor with economically-weighted parameters takes along this shape. 3 million steps was selected for the amount of iterations to run in program. When additional steps greater than 3 million was inputed, this version of the system is the first to degrade (Attractor Disintegration). The degradation of the attractor signifies that the system, due to its dependent on economical values, will eventually cease to have a form and will no longer demonstrate a pattern; this is entropy.
This is a resemblance to the current socio-economic situation globally where we are witnessing monetary injustice. The gap between the wealthy and the impoverished is increasing, and climate change is threatening the ecosystem services that maintain our ecological processes and resources. In addition, the economic system includes a process that creates an infinite input: money printing. With a system of infinite growth, it is inevitable that a catastrophe will occur and a new system will exist without the ability to revert back to its previous properties.
When the parameters are weighted towards factors that support the social system (social welfare), the system pattern becomes tighter and shows less variance. This would be an optimal situation as societies and communities would not fair well with drastic changes such as financial downturns, war, and political turmoil. A system that has a stronger attractor would also most likely be resilient to catastrophe since the system’s behaviour would be more consistent.
Similarly, when the parameters are weighted towards ecological factors (biodiversity and ecosystem services), the attractor resembles that of the socially-weighted system, but tighter. One interesting aspect is that the ecological systems also contains a process that drives an infinite input: solar radiation. One would theorize that when a system receives an infinite input, the system attractor would disintegrate. When compared to economics, ecological systems have the ability to self-organize to prevent infinite growth. All living things eventually die, trophic energies taper off due to thermodynamics, loss of energy during the transfer between trophic levels, and other evolutionary processes.